문제 정보
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The test cases are generated so that the answer will be less than or equal to 2 * 109.
Example 1:
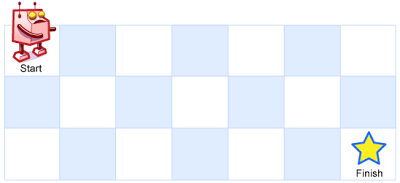
Input: m = 3, n = 7
Output: 28
Example 2:
Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down문제 풀이
DP의 두가지 조건을 만족한다. (Optimal Substructure, Overlapping Subproblem)
다음과 같이 DP로 문제 해결
1. 2차원 메모이제이션을 설정
2. 메모이제이션 맵 채우기
3. 리턴
Writeup
public class Solution {
public int UniquePaths(int m, int n)
{
int[,] memo = new int[m, n];
makeMemo(memo, m, n); //construct dp map
return memo[m-1, n-1];
}
public void makeMemo(int[,] memo, int m, int n)
{
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if(i==0 || j == 0)
{
memo[i, j] = 1;
continue;
}
memo[i, j] = memo[i - 1, j] + memo[i, j - 1];
}
}
}
}
참고로 다음과 같이 dp를 이용하지 않고 재귀로 풀면 time exceed가 나온다.
public int UniquePaths(int m, int n)
{
if (m == 1 || n == 1)
{
return 1;
}
return UniquePaths(m - 1, n) + UniquePaths(m, n- 1);
}
'Software Engineering > Algorithm' 카테고리의 다른 글
| [리트코드] 100. Same Tree (tree) (0) | 2022.01.27 |
|---|---|
| [리트코드] 94. Binary Tree Inorder Traversal (tree, recursion) (0) | 2022.01.27 |
| [리트코드] 49. Group Anagrams (HashTable) (0) | 2022.01.26 |
| [리트코드] 2011. Final Value of Variable After Performing Operations (string) (0) | 2022.01.26 |
| [리트코드] 1. TwoSum (array) (0) | 2022.01.26 |


댓글